articulo
ley de acción y reaccion
CONCEPTO: Siempre que un objeto ejerce una fuerza sobre otro objeto, el segundo objeto ejerce sobre el primero una fuerza igual y en sentido opuesto.
Una de las fuerzas se llama fuerza de acción y la otra, fuerza de reacción. No importa a cual de ellas llamemos acción y a cuál reacción. Lo importante es que ambas son partes de una sola interacción y que ninguna de las dos existe sin la otra. Las fuerzas tienen la misma intensidad y sentidos opuestos. La tercera ley de Newton se suele enunciar como : "a toda acción le corresponde una reacción de igual magnitud y en sentido contrario".
Toda fuerza que empuja la tierra hacia abajo es empujado al mismo tiempo hacia arriba
Una de las fuerzas se llama fuerza de acción y la otra, fuerza de reacción. No importa a cual de ellas llamemos acción y a cuál reacción. Lo importante es que ambas son partes de una sola interacción y que ninguna de las dos existe sin la otra. Las fuerzas tienen la misma intensidad y sentidos opuestos. La tercera ley de Newton se suele enunciar como : "a toda acción le corresponde una reacción de igual magnitud y en sentido contrario".
Toda fuerza que empuja la tierra hacia abajo es empujado al mismo tiempo hacia arriba
ECUACIÓN:
sumatoria de fuerzas en x
sumatoria de fuerzas en y
PROBLEMA DE LA 3 ERA LEY E NEWTON:
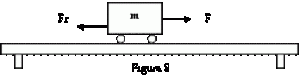
- 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema

La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
APLICACIÓN:
A toda acción hay una reacción. Supongamos que estás en un bote y tienes un remo, la fuerza que aplicas para impulsarte (acción) es de la misma dimensión pero en sentido contrario de la resistencia del agua (reacción). Otro ejemplo es tener un objeto sobre la mesa, ese objeto está estable porque el peso que tiene (acción) es igual y en el sentido contrario que la fuerza de reacción de la mesa en el libro.
simulador explicando la ley de acción y reacción:






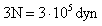



.gif)